从二进制到十进制（深入探索二进制转化为十进制的具体步骤与技巧）

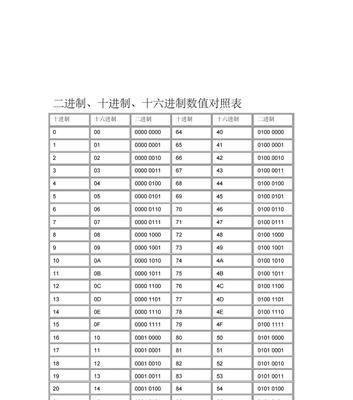
二进制和十进制是两种最常见的数字表示方法，在计算机科学和信息技术领域。而将二进制数字转化为十进制数字是我们经常需要进行的操作之一。帮助读者更好地理解和应用这一转化方法，本文将详细介绍如何将二进制转化为十进制。

二进制和十进制的基本概念

我们需要了解二进制和十进制的基本概念。而十进制则是我们平常使用的数字系统、二进制是一种由0和1组成的数字系统，由0至9十个数字组成。而十进制每位数字所代表的权值是10的幂次方递增的，二进制每位数字所代表的权值是2的幂次方递增的。

从右至左进行权值计算

将二进制转化为十进制的方法是从右至左进行权值计算。将每位数字与相应的权值相乘，并将结果相加，即从二进制数的最右边开始。对于二进制数1011，计算方法为：1*2^0+1*2^1+0*2^2+1*2^3。

权值的计算与累加

需要计算每位数字所对应的权值，在二进制转化为十进制的过程中、并将结果进行累加。表示当前位数字需要计入最后的结果中，当遇到1时；表示当前位数字不需要计入结果中，当遇到0时。通过累加得到的结果即为转化后的十进制数。

权值计算的示例演算

我们可以通过一个示例演算来进行实际操作，为了更好地理解权值计算的过程。最终得到的结果为26、分别对每位数字进行相应的计算与累加、将二进制数11010转化为十进制数时、我们按照权值计算的方法。

使用位权法进行转化

我们还可以使用位权法来进行二进制转化为十进制的操作，除了从右至左进行权值计算外。并将结果累加得到最终的十进制数、位权法是一种简化计算的方法，通过将二进制数从左至右与相应的位权相乘。

位权法转化的步骤与示例

每位计算结果累加、得到最终的十进制数、位权法的转化步骤包括从左至右按位权计算。得到的结果为21，将二进制数10101使用位权法进行转化、我们依次与位权相乘并累加。

使用公式简化计算

我们还可以使用公式来简化二进制转化为十进制的计算过程，除了以上介绍的方法外。公式为：二进制数乘以2的幂次方加和。可以直接计算出二进制数的十进制表示，通过这个公式。

公式计算的示例演算

我们可以通过一个示例演算来进行实际操作，为了更好地理解使用公式进行计算的过程。即1*2^0+0*2^1+1*2^2+1*2^3，将二进制数1101使用公式计算，最终得到的结果为13。

注意符号位的处理

我们需要注意符号位的处理，在进行二进制转化为十进制的计算过程中。0表示正数、如果二进制数是有符号数、1表示负数，则最高位为符号位。需要根据符号位的值进行相应的处理，而在进行转化时。

小数二进制转化为十进制

我们还可以将小数二进制数转化为十进制，除了整数二进制数的转化外。我们需要将小数部分的每一位数字与相应的负幂次方进行计算，并将结果累加得到最终的十进制数、在这种情况下。

小数二进制转化的示例演算

我们可以通过一个示例演算来进行实际操作、为了更好地理解小数二进制转化为十进制的过程。1101转化为十进制、并将结果累加得到最终结果为5、将二进制小数101、我们按照负幂次方计算每位数字，8125。

使用计算器或编程语言进行转化

我们可以借助计算器或编程语言来进行二进制转化为十进制的计算，在实际应用中。可以大大简化我们的操作、现代计算器和编程语言提供了二进制转化为十进制的函数或方法。

实际应用中的二进制转化为十进制

二进制转化为十进制在计算机领域中具有广泛的应用。IP地址使用二进制表示、在网络通信中、但在实际应用中需要转化为十进制才能更好地理解和使用。

二进制转化为十进制的重要性和意义

掌握二进制转化为十进制的具体方法对于计算机科学和信息技术领域的学习和应用至关重要。才能更好地进行数字计算和数据处理，只有深入理解和掌握这一转化方法。

我们可以了解到将二进制转化为十进制的具体步骤与技巧，通过本文的详细介绍。注意符号位的处理以及小数二进制转化等方法都可以帮助我们进行有效的转化，使用公式，使用位权法，从右至左进行权值计算。掌握这些方法将为我们在计算机科学和信息技术领域的学习和实践提供强大的支持。